こんにちは，数ラボの舟根です。

変な数学の参考書ばかり読んでいると思われているかもしれませんので，
本日は文庫本の紹介です。

岩波文庫から
『ガリレオ・ガリレイ　新科学対話　（上）』
『ガリレオ・ガリレイ　新科学対話　（下）』

さて，この中で私が興味をもったのは，
ガリレオ・ガリレイが「多少きつく張られた綱が，放物線によく似た曲線の形をとる。」「鎖の一端を放物線の一端に固定して垂らし，鎖を多少ゆるめると，鎖はたわんで放物線とぴったりと重なり合う。放物線の曲がりが小さいほど，鎖はこれと殆んど完全に一致する。」と主張 ( 当時の他の数学者の見解を代弁？ ) しているところです。

当時はまだ知られてはいないのですが，

関数

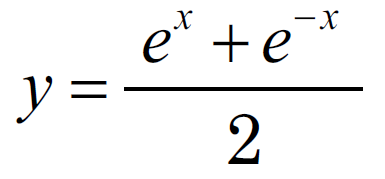
のグラフが 懸垂線 ( カテナリー ) と呼ばれる曲線になります。

グラフはこんな感じです。

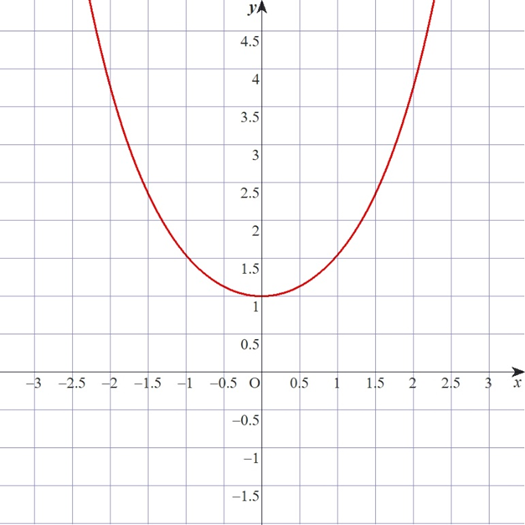
糸や鎖の両端を固定して垂らすときにできる曲線がこの曲線 ( を縦横に変倍したもの ) です。これが成り立つことを確かめるためには，軸方向，軸方向についてそれぞれ力のつり合いの式を立て，最終的に微分方程式を解くことになります。高校数学の範囲を少し飛び出してしまうこと，若干の物理 ( 力学 ) の知識を必要とすることから今回証明は割愛しますが，数学Ⅲの知識で十分理解できる内容かと思いますので，興味のある方には是非調べてみてほしいと思います。

ちなみに放物線

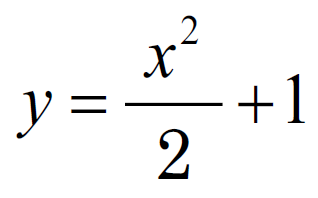
はこんな感じ。

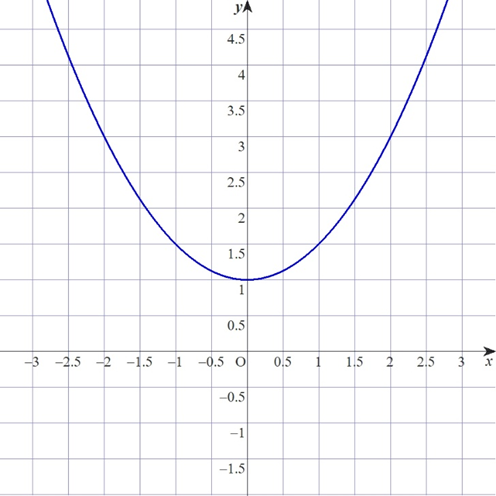
重ねてみるとこんな感じです。

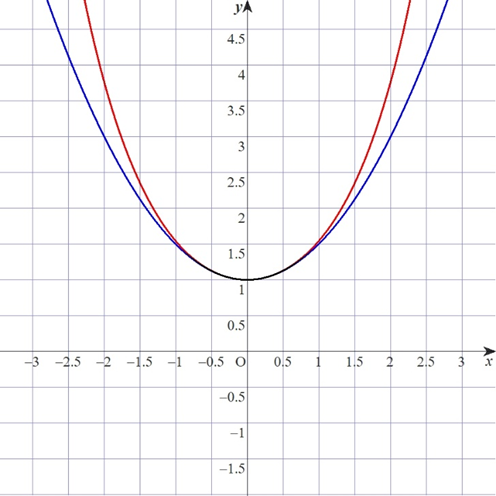
確かに似ているような気がします。

もう少し横方向の倍率を調整したら完璧に重なるようにも思えます。

もちろん懸垂線は放物線とは異なる ( 1646年，当時17歳であったホイヘンスが証明 ) 曲線なのですが，当時はまだ微分積分学，微分方程式の概念などなく，懸垂線の正体が明らかになるのはそれから約半世紀後になります。その間に数学は微分積分学の基盤を ( 別々に ) 構築した2人の天才ニュートンとライプニッツの手により爆発的に進歩し，ついに1691年ホイヘンス，ヨハン・ベルヌーイ，ライプニッツらがそれぞれ懸垂線の微分方程式にたどり着くのです。ちなみに，カテナリー ( Catenary ) という言葉の語源はラテン語で鎖の意味の“catena”で，ホイヘンスが名付けたと言われています。

そして実際に，懸垂線は頂点付近で ( マクローリン展開を用いて ) 放物線に近似することができるので，「似ている」という感覚は決して間違ったものではないのです。

大切なのは，この「似ている」という感覚と，そのような興味関心を晩年になっても抱き続けるガリレオ・ガリレイの科学者としての姿勢だと思います。

☆☆新年度説明会にぜひご参加ください☆☆

新高1向け説明会
3月26日(日)
午前の部 (10:30-11:30)
午後の部 (16:00-17:00)
高校生として最高のスタートを切るためのポイントについてお伝えします。
詳細およびお申し込みはこちらからお願いいたします。

★★春期講習のお申し込みはこちらから★★

☆☆体験授業は随時受け付けしております☆☆
数学専門塾　数ラボ https://su-labo.com/
TEL：027-328-1300